Mail
NEW

Comparing ray tracing results with approximation formula

Warning: Firefox renders the formulas correctly (Chrome and Microsoft Edge can't properly render the formula [MathM] correctly)!!!

The refraction approximation formula are quite known and coming from the astronomy, navigation and geodesy environments and are mentioned in this link. These approximation formula are (all result in [deg] or [m]):

astronomical refraction
- Sinclair (Bennett [1982, page 257], formula B at NearHeight=0m, 10°C and 1010mbar)
A s t r o R e f r a c t A T S = ( 34.46 + 4.23 * A p p A l t + 0.004 * A p p A l t 2 ) ( 1 + 0.505 * A p p A l t + 0.0845 * A p p A l t 2 ) * 60 (1)
levelling refraction (dip due vast level surface)

based on Young (Young, 2003 at 15°C and 1013.25mbar), $\begin{matrix} L e v e l R e f r a c t_{V R} = 81.945 * P / {(273.15 + T)}^{2} * (\arccos (\frac{R a + D i s t a n t H e i g h t}{R a + N e a r H e i g h t}) - \arccos (\frac{R a / (1 - K * 0.0238) + D i s t a n t H e i g h t}{R a / (1 - K * 0.0238) + N e a r H e i g h t})) & (2 \end{matrix}$ $\begin{matrix} \end{matrix}$

Nautical Almanac (2017)
$\begin{matrix} L e v e l R e f r a c t_{N A} = a r c c o s (\frac{R a + D i s t a n t H e i g h t}{R a + N e a r H e i g h t}) - 1.76 * \sqrt{N e a r H e i g h t - D i s t a n t H e i g h t} & (3) \end{matrix}$
Distance to horizon: L_ray (Young, 2003 and adjusted to map US1976: changed 3830 to 3910)
$\begin{matrix} L e v e l L_{{r a y}_{V R}} = 3910 * \sqrt{N e a r H e i g h t - D i s t a n t H e i g h t} & (4) \end{matrix}$

terrestrial refraction
- based on Thom (Thom, 1973, page 31, (3.6) at 15°C and 1013.25mbar)
T e r r e s t R e f r a c t V R = 0.00830 * L r a y * K * P / ( 273.15 + T ) 2 (5)

Simple approximation (Wikipedia and adjusted to map US1976; changed 1500 to 1300)

\begin{matrix} S i m p l e T e r r e s t R e f r a c t_{V R} = (D i s t a n t H e i g h t - N e a r H e i g h t) / 1300000 & (6) \end{matrix}

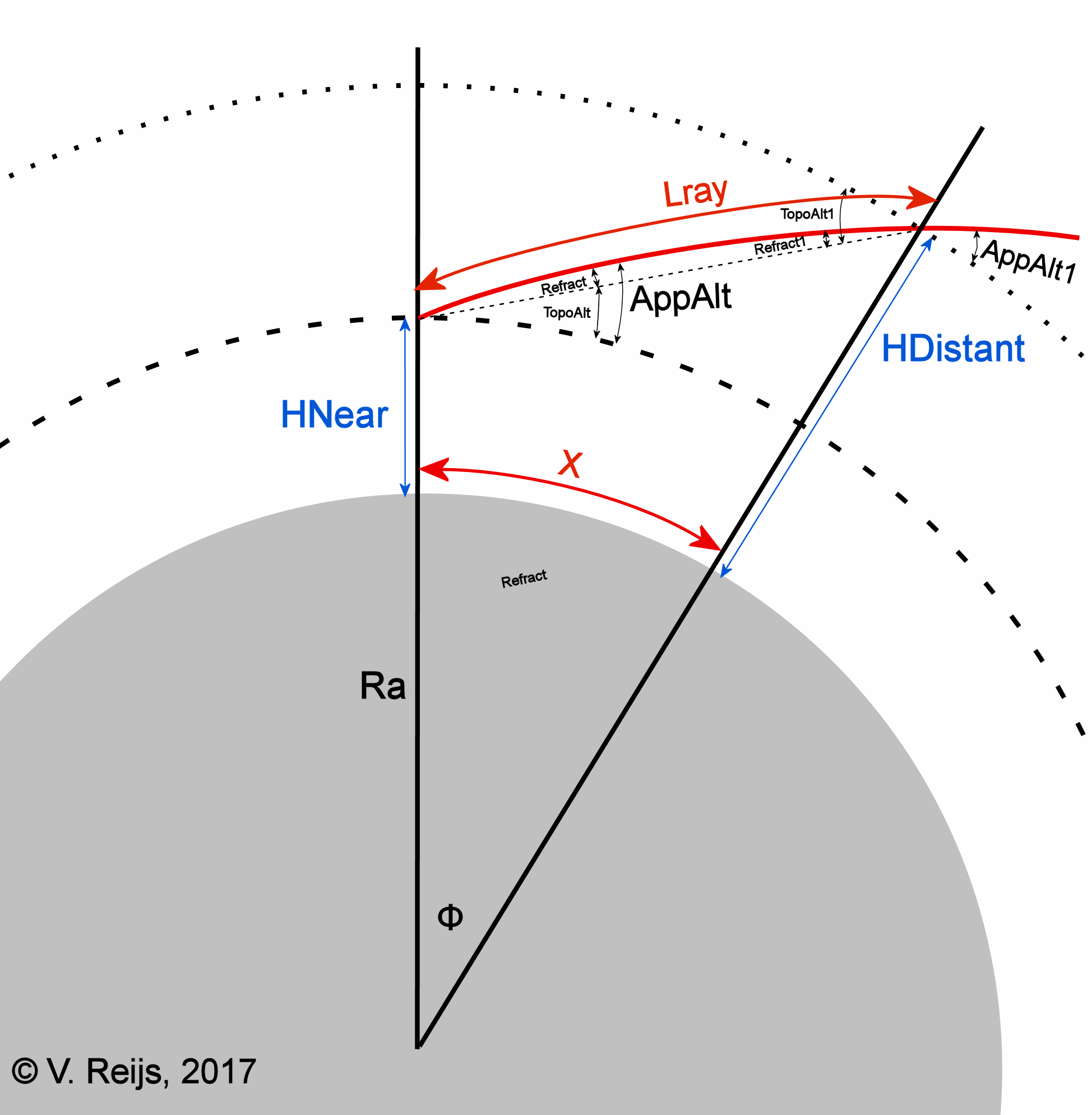
Legend
DistantHeight: Elevation of the target [m]
NearHeight: Elevation of the observer [m]
K: average Refraction Constant [-] = (0.0342 - Lapse rate) *272.84 and K=k/0.0238
Lapse rate: Average lapse rate [K/m] (remember 'Lapse rate' is the negative of 'Temperature gradient')
P: Pressure at NearHeight [mbar]
T: Temperature at NearHeight [°C]
Ra: Radius of Earth [m]
L_ray (or S): Length of the light ray [m]
X: Distance along Earth's geoid [m]
AppAlt: Apparent altitude at NearHeight [°] (AppAlt=TopoAlt+Refract)

The angles and
distances in this environmet

The angles and
distances in this environmet

The above approximation formula are compared with the results of the ray tracing implementation from Reijs: Refract_HOSI, which based on integration along apparent altitude (Hohenkerk&Sinclair, 1985). Benchmarking astronomical and levelling refraction showed that the refraction variation in results was max. 2" (around 0.05%): with integration along apparent altitude (pers. comm, Tschudin, Young, 2017) and with integration along Earth's geoid (pers. comm. van der Werf, 2017). Benchmarking terrestrial refraction was successfully spot checked with van der Werf's implementation which uses integration along the Earth's geoid (pers. comm, van der Werf, 2017).

Here are the different refraction comparisons (at 1 arcmin level, aka ~1/30 of diameter of Sun/Moon), so that we can determine the validity of the approximation functions coming from the astronomy, navigation and geodesy environments:

Astronomical refraction
The refraction is determined for a light path from the eyes' position to the end of the Earth's atmosphere (in direction of a celestial object).
Levelling refraction
The refraction is determined for a light path that has a large part level with the Earth's geoid, aka towards a vast level surface below the eyes' position. Also known as dip.
Terrestrial refraction
The refraction is determined for a light path that goes from the eyes' position to a terrestrial object higher or lower than the eyes' position.

Astronomical refraction

Under the condition of Standard Atmosphere (US1976, T₀=15°C and P₀=1013.25mbar, λ=600nm, R_earth=6378120km), the below picture provides comparison between AstroRefract_HOSI and AstroRefract_ATS (formula 1):
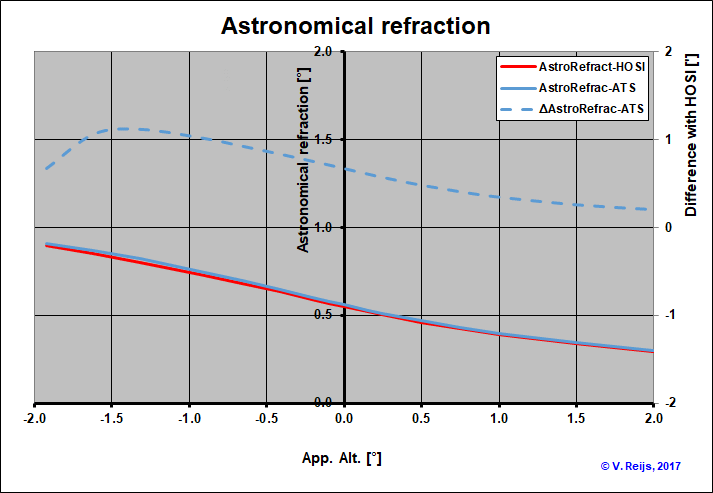
$Comparing astronomical refraction of VR's-HOSI implementationa dn Sinclair formula$

The difference between the two is max. 1.2' (blue dashed line and the right axis). This small difference is expected as Sinclair (1978) was part of the implementors of the Hohenkerk&Sincliar (1985) program (although his published formula looks to be earlier than the publish computer program).

Levelling refraction (dip due to vast level surface)

Under the condition of Standard Atmosphere (US1976, T₀=15°C and P₀=1013.25mbar, λ=600nm, R_earth=6378120km), the below picture provides comparison between LevelRefract_HOSI, LevelRefract_VR (formula 2) and LevelRefract_NA(formula 3):

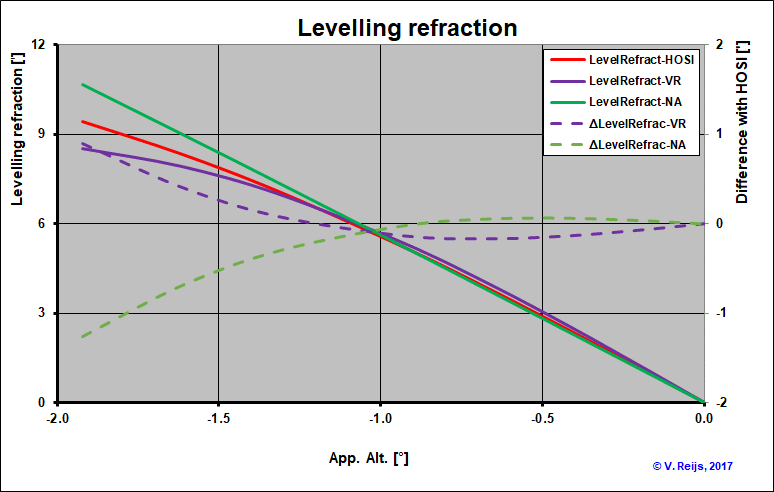
Comparing VR's
implementaiton of HOSI, VR's implementation of Thom and Nautical
Almanac.

The difference between LevelRefract_HOSI and LevelRefract_VR is max. 1' (purple dashed line and the right axis) and LevelRefract_NA is max. 1.2' (green dashed line and the right axis). They are not that far from each others (certainly below a height of 2000m, equivalent to AppAlt=-1.3°), which is expected as all are used for Standard Atmosphere (US1976) environments.

Average lapse rate or detailed height-temperature profile?

Andrew Young states: "George Kattawar and I [Andrew Young] showed that the dip depends almost entirely on the difference in temperature between the air at eye level and that at the apparent horizon, regardless of the thermal structure in between.".

Beside the temperature difference (average temperature gradient), the temperature/pressure at one of the points is important (as that also changes the refraction). So a high resolution height-temperature profile is not that important in these dip/levelling cases.

This has been tested by using two different height-temperature profiles:

The temperature starts at 15°C and stays constant up to half eye-height, and then the temperature changes gradual to eye-height. The temperature at eye-height is determined by the average lapse rate defined for each 'experiment'.
The temperature starts at 15°C and change gradual up to half eye-height and then it stays constant up to eye-height. The temperature at eye-height is determined by the average lapse rate defined for each 'experiment'.

Example: if average lapse rate is 0.0065K/m and the ground temperature is 15°C, the temperature at eye height (3000m) will be -4.5°C (=15-0.0065*3000). The slanted profile (on left side) has twice the average lapse rate (0.013K/m) up to half eye-height (1500m) and then the lapse rate is zero up to eye-height (3000m), while in the perpen[dicular] profile (on the right side) the temperature stays at 15°C up to half eye-height (1500m) and then it changes with twice the lapse rate (0.013K/m) up to the eye-height (3000m):

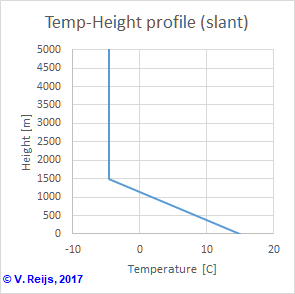
Slanted temperature change
(eye-height=3000m)

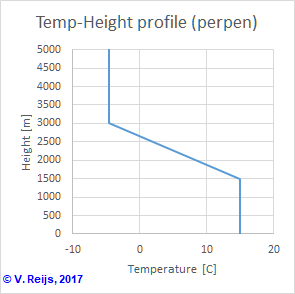
Perpendicular temperature change
(eye-height=3000m)

The temperature gradients near the horizon are thus considerable different for the two height-temperature profiles: 0.013 (slant) and 0 (perpen) K/m.

If we use these different height-temperature profiles (slant and perpen) for an average lapse rate of -0.01, 0.0065 and 0.02K/m the below picture emerges. The LevelRefract_HOSI (continuous lines) and LevelRefract_VR (dashed lines) have been calculated:
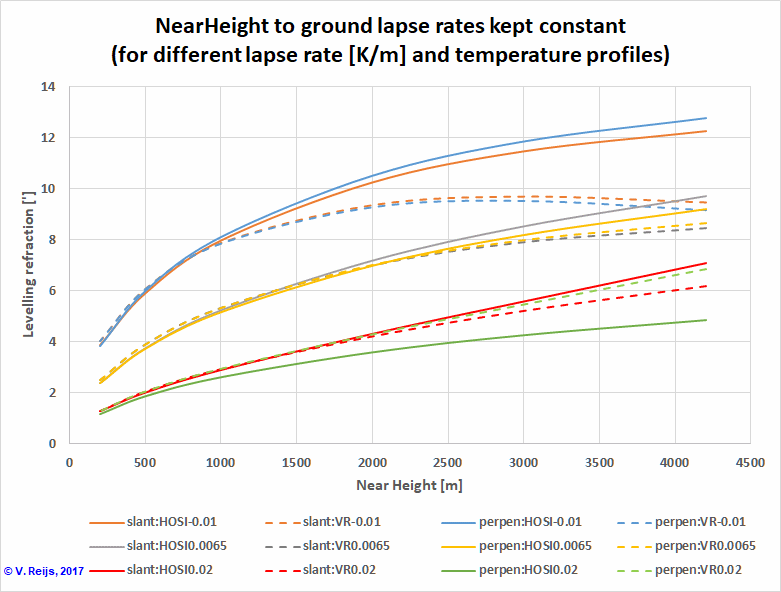
Same lapse rates with different temperature profiles

Same lapse rates with different temperature profiles

For the cases of average lapse rate 0.0065 and 0.02K/m the LevelRefract_HOSI (continuous lines) and LevelRefract_VR (dashed lines) are comparable. This is not the case for average lapse rate -0.01K/m. For some reason they diverge for higher Near Heights (>1000m). A possible reason could be because the approximation formula 2 is valid for small angles and low heights. Heights of up to 4200m were chosen because of the apparent altitude measurements of the sea level (due to dip aka levelling refraction) by Schaefer&Liller (1990).
The two different height-temperature profiles (slant and perpen) don't really produce large differences (except perhaps slightly larger differences for the average lapse rate 0.02K/m). So Andrew Young's statement looks to be correct.

Terrestrial refraction

Under the condition of Standard Atmosphere (R_earth=6378120km, T₀=15°C and P₀=1013.25mbar), the terrestrial refraction per kilometer depends on average lapse rate (remember 'Lapse rate' is the negative of 'Temperature gradient') as seen for the formula 5 and formula 6 below:
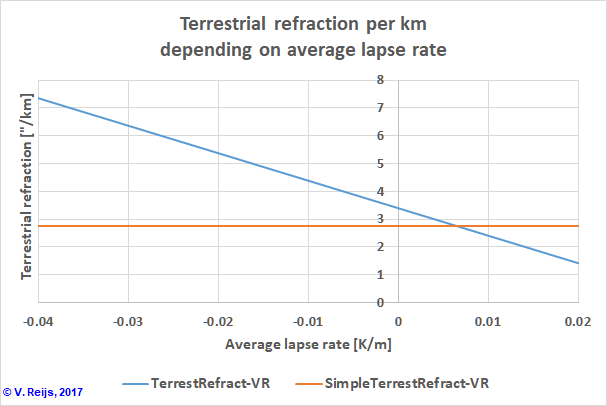
$Terrestrial refraction pe rkm$

Lapse rates of -0.04 (Stability Class=G: likely around midnight) to 0.02 (Stability Class=A: likely around noon) K/m maps Refraction Coefficients (K) of ~20 to ~4 [-]. And these are numbers that are also found through Thom's observations. The two curves cross at a lapse rate of 0.0065K/m (which is expected as the simple approximation (formula 6) is derived for 0.0065K/m only).

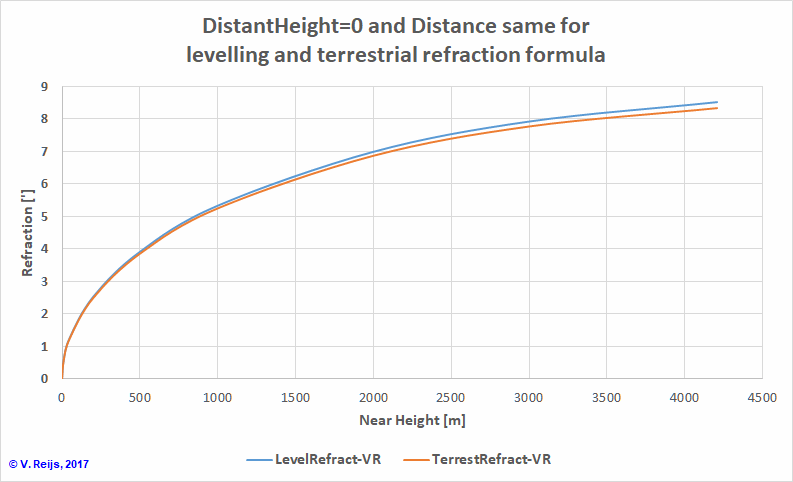
Under the condition of Standard Atmosphere (US1976, R_earth=6378120km, T₀=15°C and P₀=1013.25mbar), levelling refraction (formula 3) and terrestrial refraction (formula 5) should come to the same results if the Distance for terrestrial refraction (in formula 5: L_ray) is made the same as the level distance to horizon (formula 4) and having the same height differences. In the below figure one can see that the results are similar (within 0.2'):
$Difference between levelling and terrestrial refraction$

To determine TerrestRefract_HOSI a slight addition is needed to the ray tracing procedure. The terrestrial refraction has three parameters: H_Near, H_Distant and Distance (over Earth's geoid). The Distance (X over Earth's geoid) can be easily determined by changing Hohenkerk&Sinclair procedure to calculate the distance integral instead of the refraction integral (van der Werf, 2008, Table 1, column 2). The Apparent Altitude at the H_Near is varied (in an iterative way) so that the light ray at Distance X goes through H_Distant.

Under the condition of Standard Atmosphere (US1976, T₀=15°C and P₀=1013.25mbar, λ=600nm, R_earth=6378120km), comparing the TerrestRefract_HOSI (blue line) and TerrestRefract_VR (red line) shows that below H_Distant=1000m the two have similar behavior:
$Same lapse rates with different temperature profiles for Terrestrial refraction$
It might be that the TerrestRefract_VR (formula 5) is too much an approximation.

Using the same two height-temperature profiles as for levelling refraction (slant and perpen) for an average lapse rate of -0.01, 0.0065 and 0.02K/m, the below picture emerges for terrestrial refraction. The TerrestRefract_HOSI (continuous lines) and TerrestRefract_VR (dashed lines) have been calculated:
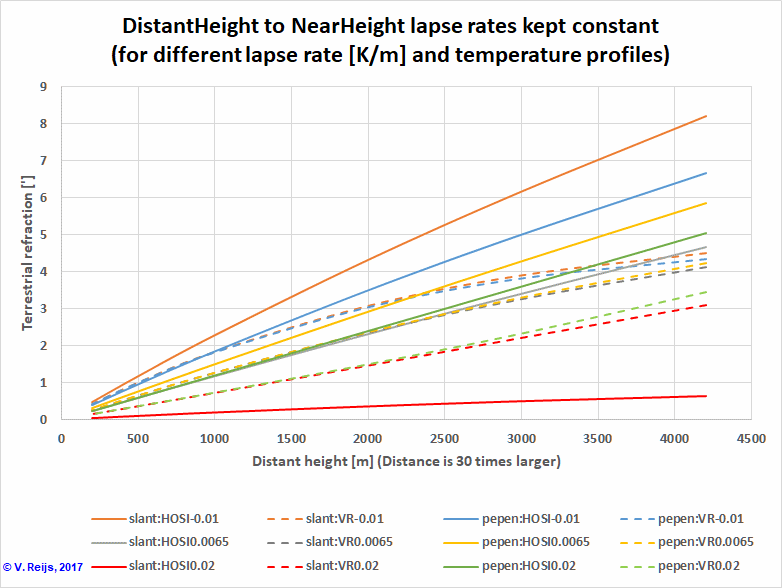
$Terrestrial refraction with different lapse rates$
The comparison for 0.02K/m is quite difficult as TerrestRefract_HOSI (green and red continuous lines) and TerrestRefract_VR (green and red dashed lines) are quite diverse, reason unknown yet. The others two lapse rates (-0.01 and 0.065K/m) are closer up to H_Distant=1000m. There might be a possibility that the approximation formula 5 is not accurate enough, so need to check that.

Conclusions

Common to all types of approximation refraction formula: below H_Distant=1000m the approximation formula and the ray tracing method give similar results, while with an average lapse rate of 0.0065K the mapping is best say up to H_Distant=2000m . This looks to be inherent to these approximation formula.

No direct evaluation has been done on changing the T₀ and P₀ at H_Near: up to now the US1976 conditions and some specific height-temperature profiles (slant and perpen) were used, but the ray tracing function can use any T₀, P₀, and height-temperature profile.

At this moment, I am not planning to determine new/other formula; as ray tracing is nowadays a simple and valid method to determine the refraction in a unified way, as was recognised in the past.

References

Bennett, G.G. 1982. 'The calculation of astronomical refraction in marine navigation', Journal of Inst. navigation, Vol 35: pp. 255-59.
Hohenkerk, Catherine Y., and A.T. Sinclair. 1985. "The computation of angular atmospheric refraction at large zenith angles." ed. by HM nautical almanac office. Cambridge.
Reijs, Victor M.M. 2007.'Refraction: Refraction calculation', in http://www.archaeocosmology.org/eng/refract.htm#Calculated [accessed 2 July 2012].
Schaefer, Brad E., and William Liller. 1990. 'Refraction near the horizon', Publications of the Astronomical Society of the Pacific, Vol 102: pp. 796-805.
Sinclair, A.T. 1978. "Data for astro-navigation in 1978 for use with small calculators." ed. by HM nautical almanac office. Cambridge.
Thom, Alexander. 1971. Megalithic lunar observatories (Oxford University Press)
Werf, Siebren Y. van der. 2003. 'Ray tracing and refraction in the modified US1976 atmosphere', Applied optics, Vol 42: pp. 354-66.
Werf, Siebren Y. van der. 2008. 'Comment on “Improved ray tracing air mass numbers model”', Applied optics, Vol 47: pp. 153-56.

Acknowledgements

I would like to thank people, such as Siebren van der Werf and others for their help and constructive feedback. Any remaining errors in methodology or results are my responsibility of course!!! If you want to provide constructive feedback, let me know.

Disclaimer and Copyright

Home

Mail

Major content related changes: December 1, 2017