Mail
NEW

Refraction

Refraction is the bending of light through the atmosphere. Three types are normally recognised in literature from astronomy, navigation and geodesy environments:

Astronomical refraction
The refraction is determined for a light path from the eyes' position to the end of the Earth's atmosphere (in direction of a celestial object).
Levelling refraction
The refraction is determined for a light path that has a large part level with the Earth's geoid, aka a vast level surface below the eyes' position is involved. Also known as dip.
Terrestrial refraction
The refraction is determined for a light path that goes from the eyes' position to a terrestrial object higher or lower than the eyes' position.

Astronomical refraction is 'coupled' in a great deal with terrestrial refraction. A celestial objects is during many times observed over a terrestrial object, and thus both the terrestrial object and the celestial object are refracted and have a common light path, and that light path can be close to the ground; certainly in case of a vast level surface (levelling refraction). Even if a celestial object is not observed over a terrestrial object the light still travel through the atmosphere.
$Angles and othe rparametrs aroudn refraction$

The largest influence of refraction is due to high temperature gradients, and these are normally the largest near the ground surface. As the light path is the longest when the light travels over a vast level surface, that situation produces the largest (variation of) refraction.

Astronomical refraction

The astronomical refraction is in many cases expressed as a function from the topocentric altitude of a celestial body.
From an old book (De sterren hemel, Kaiser, F., 1845) one can get information about the astronomical refraction. The conditions for this table are:

it is calculated over a (vast level) surface with a temperature of melting ice.

at normal air pressure.

Astronomical refraction
Apparent altitude	Astronomical refraction
^o	'
-0.5	40
0	35
0.16	33
0.32	31
0.5	29
0.66	28
0.83	26
1	24
2	18
3	14
5	10
10	5
20	2.5
30	1.5
50	.5
90	0

Or using the Sinclair (Bennett ([1982, page 257], formula B) at 10°C and 1010mbar:

AstroRefract_ATS = (34.46 + 4.23*AppAlt + 0.004*AppAlt²) / (1 + 0.505*AppAlt + 0.0845*AppAlt²)/60
 
TopoAlt = AppAlt - Refract

The inverse astronomical refraction function (with a sigma of 0.03^o) has been determined using SIMPLEX optimisation algorithm (by Victor Reijs):

InvRefract = (34.73 - 0.7711*TopoAlt - 0.0004693*TopoAlt²) / (1.119 + 0.2979*TopoAlt + 0.0316*TopoAlt²)/60

AppAlt = TopoAlt + InvRefract

With:

AstroRefract: astronomical refraction [^o]
InvRefrac: 'inverse astronomical refraction' [^o]
AppAlt.: apparent altitude [^o] of a celestial body, > -3.5^o
TopoAlt: topocentric altitude [^o] of a celestial body, > -4.5^o

For more theoretical information on astronomical refraction see: Astronomical refraction and this article.

Refraction of a terrestrial object

Two case will be presented here:

terrestrial refraction seen due to terrestrial object (like a hill, building, skyline, etc.) with a certain height above ground
levelling refraction seen due to a vast level surface (like the sea or a plane) at a low level (also called: dip).

Levelling refraction due to vast level surface

The angular depression of the apparent horizon is called levelling refraction (also known as (apparent) dip). According to Thom, A., 1973 (page 32, and changing it to metric and making air pressure and temperature explicit) the refraction due to a vast level surface is:

LevelRefract_VR = ACOS(1 / (1 + Elev / Ra)) -ACOS(1 / (1 + Elev / Ra*(1-1.8480*K*P/(273.15+T)^2)))

<most likely the P/T^2 part is outside the ACOS>

With:

LevelRefract: levelling refraction [^o]
Elev: elevation difference in [m] between observer's eyes (Near Height) and vast plane (Height Distant) (Near Height - Distant Height). Both Near and Distant Height must have same reference.
K: refraction constant K=4.91 at noon, K=10.64 during sun set/rise and night (equinox, wind speed [4 m/sec] (at 10 m height) and latitude 53°)
P: air pressure at Near Height [mbar]
T: temperature at Near Height [°C]
Ra: radius of earth = 6378137 [m]

Remember that the above does not include atmospheric conditions like extraordinary convective and inversions boundary layers. For more theoretical information on horizon dip see: Dip of the Horizon.

Terrestrial refraction

The terrestrial refraction changes the apparent altitude of a terrestrial body.
If one needs to calculate the terrestrial refraction, seen from local point, of a distant object (like the top of a mountain), the following formula is needed (from Thom, A., 1973, page 31 and changing it to metric and keeping air pressure explicit):

TerrestRefract_VR = 0.00830*K*L_ray*P/(273.15+T)^2

With:

TerrestRefract: terrestrial refraction [^o]
Elev: elevation difference [m] between point Near Height and Distant Height (Distant Height - Near Height). Both Near and Distant Height must have same reference/datum.
X: distance [km] between Near and Distant object (measured along earth's geoid)
L_ray: distance [km] between Near and Distant object (measured along the light ray)
K: refraction constant K=4.91 at noon, K=10.64 during sun set/rise and night (equinox, wind speed [4 m/sec] (at 10 m height) and latitude 53°)
The derivation of K's dependency on the lapse rate:
K = 990/2* (1/R + g) (formula (5) in Thom, 1985: with l=L and near horizontal ray path)
R =53.3 ft
g =F/ft (temp. gradient)
γ =C/m (temp. gradient)

K = 495 * (1*0.304/53.3 + (9/5)*0.304*γ)
K = 495*0.304 * (1/53.3 + (9/5)*γ)
K = 15058*9/5 * (1/53.3*(5/9) + gamma)
K = 270.9 * (0.0337 + γ) (the 0.0337 should be 0.034177: according to van der Werf, 2003, page 362)
K = 41.7 * (0.0342 + γ)/0.154
K = 41.7 * k
K = k/0.0240
P: air pressure at Eye elevation [mbar]
T: temperature at Eye elevation [°C]

Remember that the above does not include atmospheric conditions like extraordinary convective and inversions boundary layers. For more theoretical information on terrestrial refraction see: Astronomical refraction.

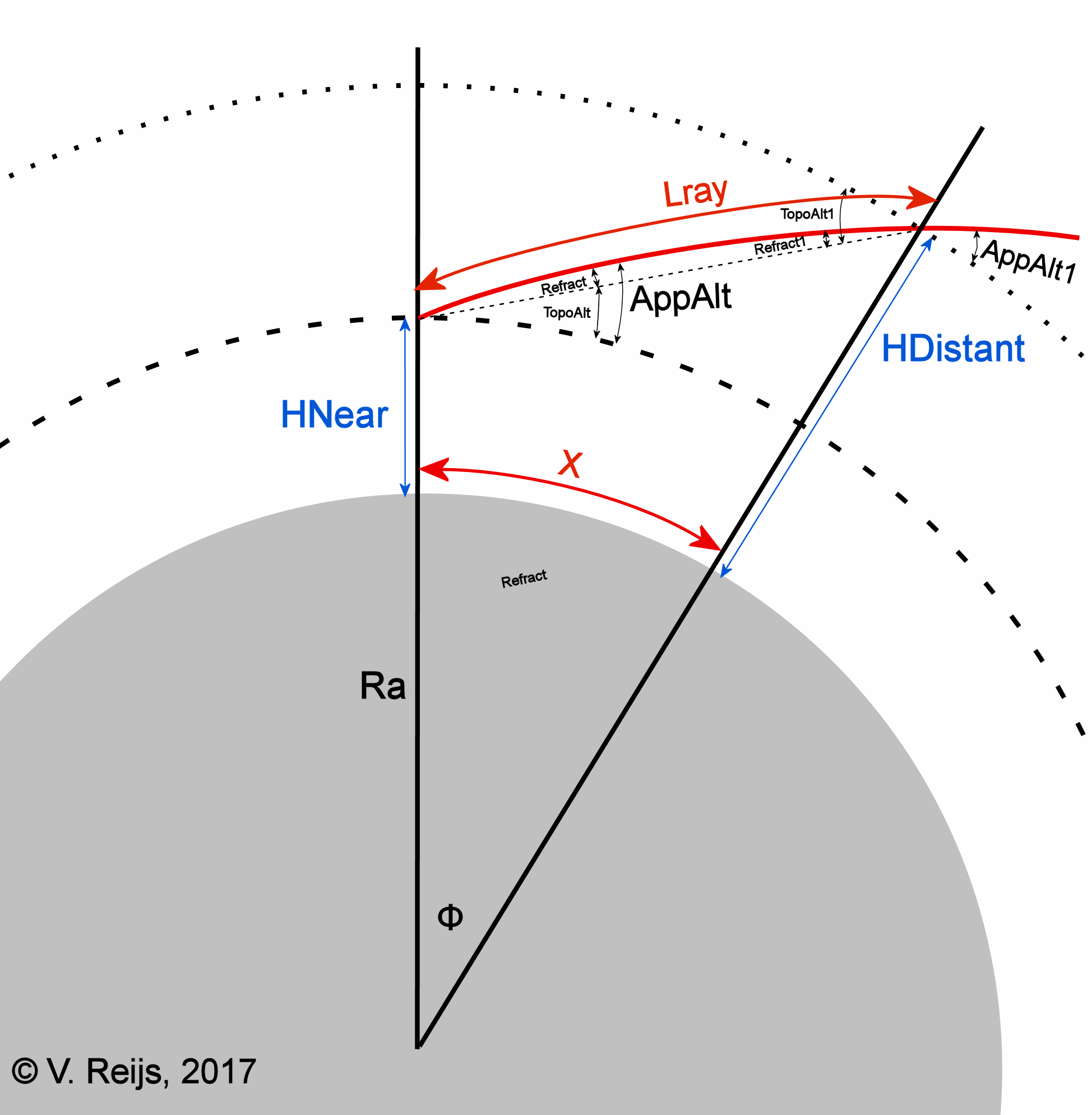
Ray tracing refraction

Using the computation method of HOSI (Hohenkerk&Sinclair, [1985]), which traces the rays by integration along the apparent altitude under the circumstances T₀=15 [C], P₀=1013.25 [mbar], RH(0)=0%, latitude observer = 50^o, remote vast level surface elevation see below (equivalent with windspeed 7.5 [m/sec]), a lapse rate at 0 [m] level compatible with the stability class, a type of surface layer H_c=1000 [m] (van der Werf, [2003], formula (52)) and MUSA76 atmosphere (van der Werf, [2003], Table 1). This method handles the astronomical, levelling and terrestrial refraction in an integral way.
The following astronomical refraction is seen due to the apparent altitude:

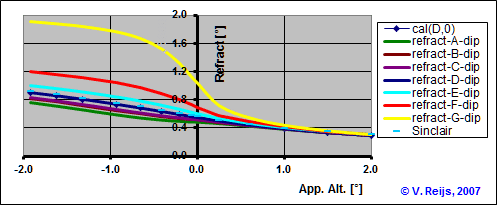
$Refraction calculated with RGO$

with the following further conditions:

In practice, the stability class will vary for Sun set/rise events mostly between D (dark blue line) to F (red line) and with lower frequency A (green) and G (yellow) can happen (C and B happen even with a lower frequency).
It is important to realise that in the above calculations, the Near Height (at the observer) has been adjust to make sure that the light path passes over the (vast level) surface. So for negative altitudes the light path is normally (but does not have to be the case! Depending on the relative elevation of observer and surface/object) over a vast level surface, for positive ones it is not coming that close to the ground and thus the temperature gradients variations are also smaller.
For the lines that have 'dip' at the end (purple [C], dark blue [D], light blue [E], red [F] and yellow [G] lines), the elevation of the observer (H_Obs) is changed to make sure that the AppAl. is equivalent to the dip (H_Obs between 4200 and 5 [m]). For apparent altitudes bigger then 0^o, the observer height was kept constant at 5 [m] above ground.
These cases would be close to actual astronomical refraction measurements as done above. The interesting is that the limiting of astronomical refraction has a somewhat comparable behavior as in the measurements.
The variation in astronomical refraction might be constant for positive apparent altitudes (PAAR) ; 'large' meaning AppAlt>0.25^o
The astronomical refraction formula of Sinclair is very close to the stability class D (dark blue) line (which uses the standard atmosphere line).
No change in H_c has been included yet. This could perhaps help in explaining the change of astronomical refraction during Sun set and rise events (the H_c is somewhat related to the atmospheric boundary layer). Although the behavior seen in Seidelmann's measurements looks not explainable using a surface layer. See here for an evaluation on surface layer.
More study is needed with regard to the boundary layer.
It might be good to also implement the computation method of van der Werf (2003). That is a slightly different method than Hohenkerk&Sinclair and Sinclair's refraction formula, as it uses integration along the geoid distance (instead of along the apparent altitude). Van der Werf allows non-spherical height-temperature profiles.
One can distinguish three apparent altitude regions (PAAR, AZAAR and NAAR) that are resulting due to variability of the temperature gradient of observation for a vast level surface.
Also the variation of the refraction does not change that much with changing negative apparent altitudes (NAAR) while the temperature gradient is constant. This looks to be due to the fact that the length of the light path close the vast level surfaces is some what independent of the value of this (negative) angle.

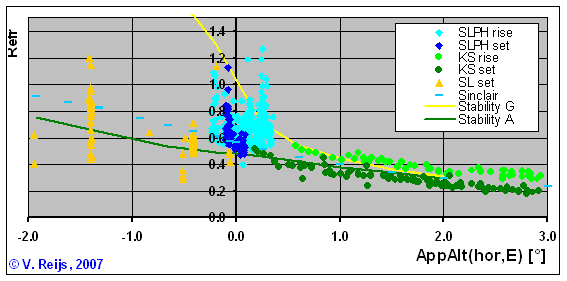
Refraction measurements

The following picture is based on refraction measurements by Schaefer&Liller (SL) [1990], Seidelmann (KS) (1968 as quoted in Schaefer&Liller [1990], page 800-801), Sampson (SLPH) [2003] and the Sinclair formula. All of these used astronomical observations that involved a vast level surface.

$Refraction observations$

The calculated curves are: Sinclair is using USA76 atmospheric model and Stability A and G use the MUSA76 atmospheric model (all calculated values are based on: 1.5m eye elevation, 15C, 1013.25mbar and 0%).
One can see an overall large standard deviation (1 sigma: ~0.15^o) in actual live and the slight difference between sun rise and set events (~0.1^o).

It is not very clear if the standard deviation will increase with lower apparent altitudes (although that is expected). For instance the standard deviation for observations around -0.4^o is 0.05^o (n=75) has a smaller standard deviation then observations at 0^o with 0.15^o (n=260), and at -1.3^o the standard deviation is higher (twice as high as at 0^o being 0.3^o (n=25). The variation (between min. and max.) looks to be the same for observation at apparent altitude of -1.3^o and 0^o: around 0.8^o degrees. Looks to be some limiting going on. Looking at the below calculations the deviation might indeed stay more or less the same for negative apparent altitudes. The possible calculated limiting stability classes A and G are given.

Not enough data points are available to see if there is a significant difference, the below calculations might give some insight.

Calculating the effects of refraction on apparent altitude

Browser should support JavaScript (see here for description of these functions)

General parameters

Air pressure:   [mbar] (at eye- orsea-elevation reference)
Temperature:    [^oC] (using same elevation reference as Air pressure)
Time of day:   sun set/rise or night (latitude 53° and windspeed 4 [m/sec] (at 10 m height))
               noon at equinox (latitude 53° and windspeed 4 [m/sec] (at 10 m height)) 
               standard atmosphere 
               sun set/rise or night at average windspeed of  +/-  [m/sec] (at 10 m height)
               own K:  +/-  [-]

There are some useful conversions available!

Altitude due to astronomical refraction

Apparent altitude:  [^o]

The apparent altitude value could be the apparent altitude of a distant object or the vast level surface.

altitude of celestial object: [^o]

Apparent altitude of distant object due to terrestrial and levelling refraction

Near Height: , Distant Height:  +/-  [m]
Distance X:    +/-  [km]

apparent altitude of distant object (terrestrial refraction): +/- [^o]
apparent altitude of vast level level (leveling refraction): +/- [^o]

Useful conversions

  [^oF]      [feet]   [mile]     [in Hg]      [mm Hg]   
 of the above :
[^oC]  [m]  [km]  [mbar]  [mbar]

Measurements in the above environment

Remember that if one measures the altitude with a clinometer, altimeter or sectant; one always measures the apparent altitude! If using values from maps or GPS, one has to calculate the apparent altitude using the above terrestrial or levelling refraction.
For determining the declination of the celestial body one needs the (geocentric) altitude.
So when combining the above things (like when calculating the declination), one has to remember the above formulae for celestial and terrestrial bodies.

Acknowledgments

I would like to thank the following people for their help and constructive feedback: Catherine Hohenkerk, Geoffrey Kolbe, Russell Sampson, Bradley Schaefer, Miles Standish, Marcel Tschudin, Siebren van der Werf and Andrew Young and all other unmentioned people. Any remaining errors in methodology or results are my responsibility of course!!! If you want to provide constructive feedback, let me know.

Disclaimer and Copyright

Home

Mail

Last content related changes: July 22, 2000