Mail
NEW

Hohenkerk&Sinclair implementation improvements

An implementation has been made of Hohenkerk&Sinclair (1985) around 2006. This included a few improvements (they are using ARCHAECOSMO package, see here for description of these functions):

my Visual Basic (VBA) has a number precision of 15 decimal digits.
is based on A_W formula (Werf, 2003, formula 23), which has fixed difference of 11.2684 between A_D and A_W
is based on analytic power law (PL2) saturated vapor pressure (Hohenkerk&Sinclair, 1985)
Nautical Almanac formula for gravity (Explanation supplement to the astronomical almanac. 1992)
use a constant gravity (g_mid) within each layer (mid layer gravity: instead of bottom) of the troposphere and the stratosphere
R_Earth is based on WGS84
slightly adjusted physical constant (M_W=18.016)
stratospheric atmosphere is handled in the same way as troposphere atmosphere
a constant Relative Humidity (RH) within each layer of the troposphere and the stratosphere.
both positive and negative lapse rates are supported
beside astronomical refraction (whole path); also allowed to do refraction integration over part of the ray so terrestrial and leveling refraction can be calculated.
allow for negative apparent altitudes (through leveling refraction and bisection method)
the Newton integration has been made depending on the conversion status (and not limited to 4 steps, but limited to 500 steps).
added improved Ciddor A_D formula (Werf, 2003, formula 21)
split large layers into sublayers to make sure that integration works as accurate as possible (as it better incorporates the variability of gravity): gave some change in case there are only a few layers (within 3arcsec at RH=0% and RH=75%)

In 2017/2018 several improvements were made together with van der Werf and Tschudin, to allow benchmarking between the different implementations and to improve each other's implementations (the recent improvements over the ARCHAEOCOSMO package (2006) have been checked at (small) negative and positive apparent altitude for astronomical refraction):

Hinze's formula for gravity (plus improvement of Tschudin) (Hinze, 2005): gave no significant change (within 2arcsec at RH=0%)
slightly adjusted physical gas constant (GCR=8314.4598): gave no significant change (within 1arcsec at RH=0%)
included Ciddor A_W formula (Werf, 2003, formula 24), to replace the fixed 11.2684 of A_D-A_W: a more recent formula, significant change (around -4.5arcmin at RH=75%)
incorporated in dn/dr in an analytic way for two other saturated water vapor pressure formula Ciddor CC2&CC4 (van der Werf, 2003, formula 27&28): a difference of +3&+5arcmin compared to PL2 (with inversion and RH=75%).
able to handle one duct: enhanced the use of the implementation.
integration not only for refraction but also: height, distance along geoid (or PHI angle), ray length and airmass (van der Werf, 2008): enhanced the use of the implementation
added feature to calculate terrestrial refraction from NearHeight to DistantHeight at a certain distance (using bisection method): enhanced the use of the implementation

Benchmark cases

Several implementation were benchmarked with different HT-profiles:

inversion and presence of duct (α=-0.3K/m [between 200 and 250m], eye height=350m and RH=0%)
within a few arcsec for the implementations of: Young, van der Werf, Tschudin and Reijs
inversion (α=-0.125K/m [between 0 and 50m], eye height=50m and RH=75%)
The accuracy of the three implementations is within arcsecs for the PL2 water vapor pressure. For CC2&CC4 water vapor pressure, the accuracy is less; within arcmins (at relative small neg. apparent altitudes) for the implementations of: van der Werf, Tschudin and Reijs.
The seen result differences are much larger than the next inversion case; due to the fact that in this high -0.125K/m inversion case the light-ray radius is close to R_Earth.
inversion (α=-0.11K/m [between 0 and 50m], eye height=50m and RH=75%)
within 15 arcsecs for the implementations of: van der Werf, Tschudin and Reijs
superadiabatic (α=+0.03K/m, α=+0.1K/m or α=+0.14K/m [between 0 and 50m], eye height=50m and RH=75%)
within an arcsec for the implementations of: van der Werf, Tschudin and Reijs

There are videos made of these benchmark cases (for different wavelength Red, Green and Blue: 0.532, 0.650, 0.473µm)

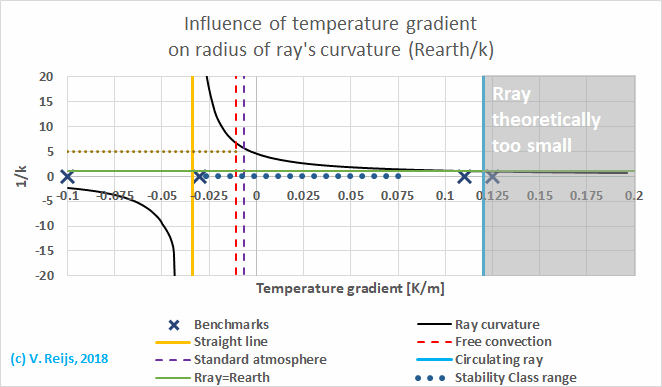
Ray's
radius curvature with regard to temperature gradeint
Remember in above graph: the lapse rate (α) is the negative of Temperature gradient (k=(0.034+Temperature gradient)/0.154)

Implementation formula

Variables and their values and/or dimensions:
δ: 18.36
R_a: 6378137m
R_c: 6356752.3m
M_D=28.964
M_W=18.016
GCR=8314.4598
T [K] between bottom and top of layer
T₁ [K] at bottom of layer
T₂ [K] at top of layer
h [m] between bottom and top of layer
h₁ [m] at bottom of layer
h₂ [m] at top of layer
α: lapse rate [K/m] (T₁-T₂)/(h₂-h₁)
g [m/sec]
g_mid [m/sec] at middle of layer
Latitude: [rad] (geocentric; might be better to use geographic/geodetic latitude which is directly related to WGS84)
RH:0-1 is constant in the layer
λ wavelength [µm]
P [mbar] between bottom and top of layer
P₁[mbar] at bottom of layer
P₂[mbar] at top of layer

Warning: Firefox renders the formulas correctly (Chrome and Microsoft Edge can't properly render the formula [MathM] correctly)!!!

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} γ = \frac{M_{D} * g_{m i d}}{GCR * α} & (1) \end{matrix}

From Hinze (2005):

\begin{matrix} g_{b a s e} = 9.7803267715 * \frac{1 + 0.001931851353 * \sin^{2} (L a t i t u d e)}{\sqrt{1 - 0.0066943800229 * \sin^{2} (L a t i t u d e)}} & (2) \end{matrix}

From Hinze (2005):

\begin{matrix} g_{h} = - 0.00001 * (0.3087691 - 0.0004398 * \sin^{2} (L a t i t u d e) * h + 0.000000072125 * h^{2}) & (3) \end{matrix}

From Tschudin (2017):

\begin{matrix} g_{a t m} = - 0.00001 * e^{(- 0.000000000865662 * h^{2} - 0.000122514 * h - 0.127137)} & (4) \end{matrix}

\begin{matrix} g = g_{b a s e} + g_{h} + g_{a t m} & (5) \end{matrix}

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} P_{W_{P L 2}} (T, R H) = R H * {(\frac{T}{247.1})}^{δ} & (6) \end{matrix}

From van der Werf (2003, formula 27):

\begin{matrix} P_{W_{C C 2}} (T, R H) = R H * e^{(21.39 - 5349 / T)} & (7) \end{matrix}

From van der Werf (2003, formula 28):

\begin{matrix} P_{W_{C C 4}} (T, R H) = R H * e^{(0.000012378847 * T^{2} - 0.019121316 * T + 29.33194026 - 6343.1645 / T)} & (8) \end{matrix}

Slightly adjusted from van der Werf (2003, formula 23):

\begin{matrix} A_{W_{H o S i}} (λ) = (24580.387 + \frac{162.88}{λ^{2}} + \frac{1.36}{λ^{4}}) * \frac{273.15}{1013.25} * 1 0^{-8} & (9) \end{matrix}

From van der Werf (2003, formula 24):

\begin{matrix} A_{W_{C i d d o r}} (λ) = (295.235 + \frac{2.6422}{λ^{2}} - \frac{0.03238}{λ^{4}} + \frac{0.004028}{λ^{6}}) * \frac{293.15}{13.33} * 1.022 * 1 0^{-8} & (10) \end{matrix}

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} A_{D_{H o S i}} (λ) = (28760.4 + \frac{162.88}{λ^{2}} + \frac{1.36}{λ^{4}}) * \frac{273.15}{1013.25} * 1 0^{-8} & (11) \end{matrix}

Slightly adjusted from van der Werf (2003, formula 21):

\begin{matrix} A_{D_{C i d d o r}} (λ) = (\frac{5792105}{238.0185 - λ^{-2}} + \frac{167917}{57.362 - λ^{-2}}) * \frac{288.15}{1013.25} * 1 0^{-8} & (12) \end{matrix}

From this link -->

\begin{matrix} R_{E a r t h} (L a t i t u d e) = \frac{1}{\sqrt{{(\cos (L a t i t u d e) / R_{a})}^{2} + {(\sin (L a t i t u d e) / R_{c})}^{2}}} & (13) \end{matrix}

Using law of Dalton:

\begin{matrix} P_{T} (T) = P_{D} (T) + c * P_{W} (T) & (14) \end{matrix}

The below c-formula is an approximation (as it looks to be related to formula 6: power law P_w(T) formula)

\begin{matrix} c = - (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} & (15) \end{matrix}

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} P_{T} (T) = P_{D} (T_{1}) * {(\frac{T}{T_{1}})}^{γ} + c * P_{W} (T) & (16) \end{matrix}

\begin{matrix} P_{T} (T) = (P_{T} (T_{1}) - c * P_{W} (T_{1})) * {(\frac{T}{T_{1}})}^{γ} + c * P_{W} (T) & (17) \end{matrix}

\begin{matrix} P_{T} (T) = (P_{T} (T_{1}) + (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} * P_{W} (T_{1})) * {(\frac{T}{T_{1}})}^{γ} - (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} * P_{W} (T) & (18) \end{matrix}

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} T (h) = T_{1} - α * (h - h_{1}) & (19) \end{matrix}

From van der Werf (2003, formula 19):

\begin{matrix} n (T) = 1 + A_{D} * P_{D} (T) / T + A_{W} * P_{W} (T) / T & (20) \end{matrix}

From Hohenkerk&Sinclair (1985, 4):

\begin{matrix} n (T) = 1 + A_{D} * P_{T} (T) / T - (A_{D} - A_{W}) * P_{W} (T) / T & (21) \end{matrix}

\begin{matrix} \begin{array}{l} n (T) = 1 + A_{D} * (P_{T} (T_{1}) + (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} * P_{W} (T_{1})) * {(\frac{T}{T_{1}})}^{γ} / T + \\ - (A_{D} * (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} + A_{D} - A_{W}) * \frac{P_{W} (T)}{T} \end{array} & (22) \end{matrix}

Partly from Hohenkerk&Sinclair (1985, 4):

\begin{matrix} \begin{array}{l} \frac{ⅆ n}{ⅆ h} = \frac{ⅆ n}{ⅆ T} * \frac{ⅆ T}{ⅆ h} = - α * A_{D} * (P_{T} (T_{1}) + (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} * P_{W} (T_{1})) * {(\frac{T}{T_{1}})}^{γ - 2} * (γ - 1) / T_{1}^{2} + \\ + α * (A_{D} * (1 - \frac{M_{W}}{M_{D}}) * \frac{γ}{δ - γ} + A_{D} - A_{W}) * \frac{d (P_{W} (T) / T)}{ⅆ T} \end{array} & (23) \end{matrix}

Using the quotient rule of differentiation:

\begin{matrix} \frac{d (P_{W} (T) / T)}{ⅆ T} = \frac{T * \frac{d (P_{W} (T))}{ⅆ T} - P_{W} (T)}{T^{2}} & (24) \end{matrix}

Preferred formula:

For P_W: formula 8, and not 6 or 7
For A_W: formula 10, and not 9
For A_D: formula 12, and not 11

References

Hinze, W. J., C. Aiken, J. Brozena, B. Coakley, G. Flanagan, R. Forsberg, T. Hildenbrand, and G. Keller, Randy. (2005) New standards for reducing gravity data: The North American gravity database. Geophysics, Vol. 70, pp. J25-J32.
Hohenkerk, Catherine Y., and A.T. Sinclair. 1985. "The computation of angular atmospheric refraction at large zenith angles." ed. by HM nautical almanac office. Cambridge.
Seidelmann, P. K. (1992) Explanatory Supplement to the Astronomical Almanac. University Science Books.
Werf, S. Y. v. d. (2003) Ray tracing and refraction in the modified US1976 atmosphere. Applied optics, Vol. 42, pp. 354-366.
Werf, S. Y. v. d. (2008) Comment on “Improved ray tracing air mass numbers model”. Applied optics, Vol. 47, pp. 153-156.

Acknowledgements

I would like to thank people, such as Marcel Tschudin, Siebren van de Werf and others for their help and constructive feedback. Any remaining errors in methodology or results are my responsibility of course!!! If you want to provide constructive feedback, let me know.

Disclaimer and Copyright

Home

Mail

Major content related changes: December 5, 2017