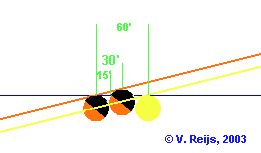Home
Home Up
Up Search
Search Mail
Mail
NEW

Under construction (like life itself)
Investigating the major standstill limit event in 2024/2025
The following subjects are handled on this page:
Project goals
In 2024/25 a major declination standstill limit of the Moon will
happen again (happens on average every 18.61 years) and this web
page will possibly report on the observations of the 2024/25 event
around the world. This is a followup of the 2006 major
standstill limit project.
Short
explanation of the major standstill event
The following sites/ideas/questions will be covered:
- Many locations in the world, where lunar standstill limit
observations could have occurred in former times, will be
studied. At this moment the following locations will be covered:
If you want to do things at the same or other locations, let me know!
- Be aware that the difference between geocentric major
(declination) standstill limit and apparent major
azimuth standstill limit can be a multiple of tropical months.
Different locations (longitude/latitude) on earth can also have
different sequences of apparent major azimuth
standstill dates (due to the fast moving Moon along its orbit).
- Most lunar phases around the major azimuth standstill limit
are between
20 to 70%, as know by theory that quarter Moons are
close to a major standstill limit.
- Full-ish
Moons (75-100%) are not really present in say this top 5,
but will be covered by the investigations, because of the
possible ritual use of full Moon.
- Can the above mentioned lunar phases be observed under all
circumstances (day/night time and low apparent altitudes), and
how could they be utilized in former times? If possible a
theoretical model would be nice (like an extension of visibility ideas),
if not possible than pragmatic rules of thumb would be a welcome
outcome.
- The shape of the
Moon (due to its phase) also influences the date of the
observed limits.
- Investigate if rise, set, meridian transit, reappearing or
other events were important at the locations.
- Determine the influence of actual (and changeable) astronomical
refraction on the sequence of the event dates (accurate
measurement equipment needed like theodolite).
- Get an idea how the events would have been experienced in former times (say
3000 BCE), also taking in account the change of obliquity.
- Determine the best way to predict, calculate and record the
set/rise/meridian transit/etc. events.
- How is the relation with the
tides.
- Understand/find existing literature/history/ethnography
(including web-pages) on this subject.
- Report on the web and other methods about the results of these
investigations.
In the below text more context is given about the issues around the
major azimuth standstill events.
Definitions
Important: There is a difference
in the major/minor standstill limits in declination (which is the
definition of geocentric major/minor standstill limit) and
the definition about apparent major/minor azimuth
standstill limit. This is because the rise/set moments of the Moon
do not necessarily have to be the same moments as reaching the
extreme declination. The same phenomena will change dates due to
changing observation location (longitude/latitude). See this link
for more info.
The standstill limit is determined by the lunar inclination and
perturbation. All these three cycles are not maximum/minimum at the
same moment, so the Moon's declination only rarely reached it
maximum/minimum.
A few definitions are handy for lunar standstill limit events in a
certain epoch:
- theoretical
standstill limit
A theoretical moment when the Earth's obliquity, lunar
inclination and perturbation are all at their maximum/minimum.
The geodentric declination for 2024/2025 is 28.74°
(or -28.74°).(ARCHAEOCOSMO)
- geocentric (or real) standstill limit event
The geocentric standstill limit event happens at the
moment the declination is at its maximum/minimum in that epoch
(will be slightly different than theoretical standstill
limit). The Moon does not have to be at a rise/transit/set
position.
The geocentric declinations belonging to these geocentric
standstill limit events are in Meeus ([1997], table 5A or ARCHAEOCOSMO.
- apparent standstill limit event
At the rise/transit/set position of the Moon, the declination
and thus azimuth can be slightly different from the geocentric
standstill limit. This apparent azimuth can be
observed.
This is depending of the
location on Earth and calculated using JPL or ARCHAEOCOSMO.
Phase periods
The phase periods (each period is almost 7 days in length) used in
the below text are as follows (pictures of the Moon are at meridian
transit moments):
- start new-ish Moon (0%)
- end of new-ish and start quarter-ish Moon (25%)
-
 or
or 
- end quarter-ish and start of full-ish Moon (75%)
-
 or
or 
- end full-ish Moon (100%)
The lunar azimuth standstill limit
determination
As already studied earlier,
determining the date of the geocentric major azimuth
standstills limit is not easy. From that study, the window of 0.4°
is there due to the fluctuation of the azimuth value of the major
azimuth standstill limit over a long period (many cycles).
Furthermore the astronomical
refraction will change the azimuth of set/rise point
(certainly for apparent altitude below 1 degree). Between
winter (1030 mbar, 0°C) and summer (990 mbar, 20°C) the difference
in refraction can be ~0.07° (which is a small estimation; in
real practice it can be larger, up to
30% of the nominal value) in apparent altitude. A
change of apparent altitude of ~0.07° translates into a
change in azimuth of around 0.3° at winter solstice and latitudes
of 59° (for lower latitudes and away from winter solstice this
change becomes smaller).
So all in all it is very difficult to determine precisely the date
of the geocentric major azimuth standstill limit using a
megalithic building.
Another way of looking at it, is looking at the calculated
azimuth on different dates and different locations for months
around the geocentric major azimuth standstill limit
date. This was done for Calanais I
(Lewis, Scotland).
The major azimuth standstill limits found, change slightly per
location and rise/set event:
- apparent northern major azimuth standstill limits:
- Sept. 24th, 2024 (Calanais I rise&set)
- apparent southern major azimuth standstill limits:
- March. 22nd, 2025 (Calanais I rise&set)
Findings on azimuth standstills limits
Apparent limits at rise and set
The apparent northern major azimuth standstill limit on
Sept. 24th, 2024 and the
apparent southern major azimuth standstill limit
happens on March 22nd, 2025. But from the above one can
also deduct that other dates are very close (at least using JPL and
linear interpolation). For this location and epoch; the geocentric
events happens on the same dates as the apparent events.
If we take into account the 0.3° window of astronomical refraction,
we have at least 4 to 5 dates in that azimuth range (these entail a
period of ~1 year, with intervals between the dates of multiples of
the lunar tropical month (average
~27.32 days).
This idea is also mentioned by Thom ([1973],
page
18):
"The Moon, it is true, in no sense stands still, but for about a
year the limiting declinations do not vary more than 20 arc
minutes, so that for month after month the Moon's declination goes
through almost the same cycle."
The theoretical, geocentric and apparent azimuth
standstill limits
For the 2024/2025 epoch the following theoretical, geocentric
and apparent azimuth standstill limits were
calculated (AppAlt=0.93° of Moon's centre at first/last gleam and
latitude Calanais I: 58.2015°):
Event
|
Theoretical
standstill limit
GeoDecl/Azi
|
Geocentric
standstill limit
GeoDecl/Azi
|
Apparent
standstill limit
GeoDecl/Azi
|
Northern rise
|
28.73°/29.43° |
28.72°/29.47° |
28.62°/29.80° |
Southern set
|
-28.73°/197.44° |
-28.73°/197.45° |
-28.70°/197.58° |
Meridian transit
The dates when the maximum and minimum meridian transits happen are
also different from the (geocentric/apparent) azimuth
and (theoretical) declination standstill events, see Appendix
III.
Phase distribution
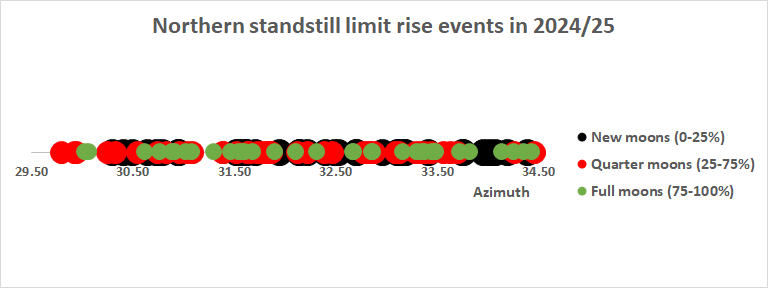
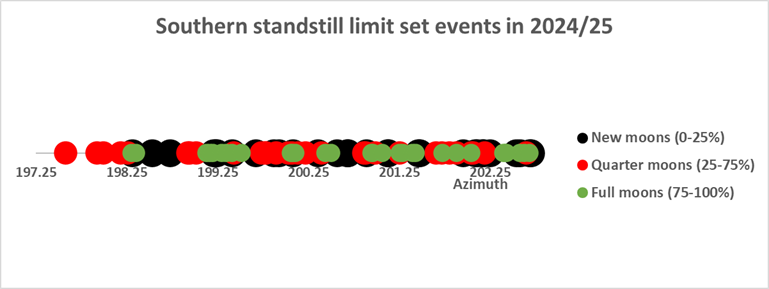
The distribution of phases near the apparent northern and
southern standstill limit azimuth for example Calanais I can be seen
below (azimuth calculated is of centre of the Moon):
In both cases: quarter-ish Moons happen closer to the geocentric
northern azimuth (for 2024-2025 epoch), followed by full-ish
Moons and new-ish Moons.
The apparent major azimuth standstill limits (for
2024-2025 epoch) though are respectively 197.6° and 29.8° and the
difference to the first full-ish Moons is respectively some 0.7°
and 0.2°.
Remember this is only an example, other locations can have
different values and sequences.
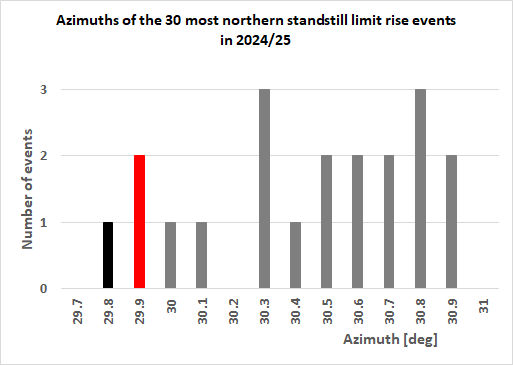
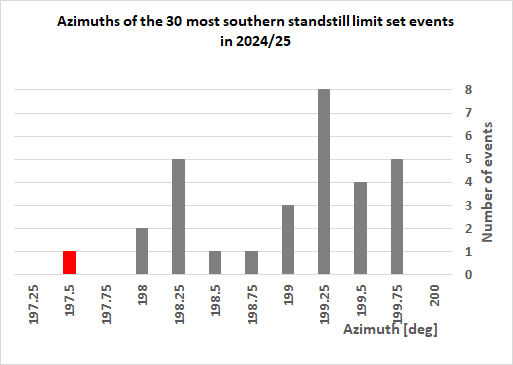
Azimuth distribution
If one takes the 30 most apparent northern and southern
Moons one gets the below distribution regardless of the
twilight/darkness conditions and azimuth calculated for centre of
the Moon:
This could provide an idea how alignments will be distributed when
looking at Moons (any observable phase over a spans of 2.5 years),
so this includes ritual aspect (full-ish Moon) and the proto-scientific
aspect (quarter-ish Moons), for the 2024-2025 epoch (at Calanais I).
Over these 30 southern and northern standstill events one gets
respectively an average azimuth of
199.0° +/- 0.6° and 30.7° +/- 0.4°, while the lowest apparent major
azimuth standstill limit (for 2024-2025 epoch) are respectively at
197.6° and 29.8°. So a difference of respectively 1.4° and 0.9°.
The total error in lunar azimuth (near standstill limit and close
to Calanais I), is a combination of (1degree in altitude change
into approximately 4 degrees in azimuth):
- uncertainty of which azimuth event is recorded by the
monument (so full-ish to quarter-ish Moons): 1s=0.5° [average]
- uncertainty if the altitude: lower limb, centre or upper limb
of Moon was used: 1s=0.33° (0.5°
[full range]/6 [1 sigma in altitude]*4)
- uncertainty about the astronomical refraction: 1s=0.2° (0.3° [full range]/6 [1 sigma in
altitude]*4)
- uncertainty about the value of the azimuth standstill limit
when looking over multiple periods of 18.61 years:
1s=0.1° (0.4° [full range]/6 [1 sigma
in azimuth])
So when measuring the average alignments of a lot of monuments,
assumed to be directed to azimuth standstill limit, a resulting
error of around 0.6° would be expected to be seen.
Favoured Moon set/rise event at
minor/major azimuth standstill events
North
The below text is copied from North [1996],
page
564-567:
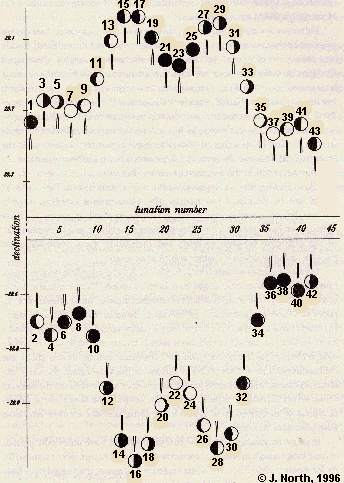
Fig. 209. Extreme values on the graph of the
Moon's declination for a typical series of lunations
around major northern and southern standstills.
The period covered is about 43 months. The lunations
are numbered consecutively and the approximate
phase of the Moon is shown for each.
The new Moon is strictly unobservable, lost as it is in the
glare of the Sun. Although the Moon becomes visible within a day
or two of new Moon, the general insignificance of corresponding
declinations (and thus azimuths) when it does so is noteworthy
(see the points marked 6, 21, 23, 25, 34, 36). Although Semitic
peoples have attached great religious importance to the first
observation of the lunar crescent after the new Moon, they have
taken no particular notice, as far as can be seen, of lunar
standstills.
The quarters give more or less the true extremes. At first
quarter (the disc is shown blackened on the left half) the Moon
has passed the Sun in ecliptic longitude by about 90°, so the
Sun is high in the sky when the Moon rises, but has set long
before the Moon sets. Only under very special atmospheric
conditions is this Moon rise visible. At third quarter, it is
only the rising of the Moon that is likely to be visible.
Full Moon is a conspicuous event, notable in its own right, and
observations of its occurrence on the horizon could have been
observed if they fitted readily into the scheme of standstills.
Consider the alternatives: roughly speaking, if the Moon is on
the horizon at full, then the Sun cannot be far from the
opposite horizon. As far as visibility is concerned, refraction
and parallax are of much less importance than the difference in
declination of the Sun and Moon. In cases 7 and 37, at the
winter solstice, the Moon is to the north of the ecliptic degree
opposite the Sun, so that when the Moon is on the horizon,
whether rising or setting, the Sun is a few degrees above the
opposite horizon. In both cases the Moon is difficult to see. In
cases like 22, however, with the Moon south of the ecliptic, it
sets before the Sun rises, and rises after sunset.
This describes the ideal situation, but winter full Moons like
7 and 37 should not be dismissed too readily. The Moon moves
rapid, roughly thirteen degrees per day, and a day on either
side of full Moon makes little difference to its declination,
but through change in ecliptic longitude can make all the
difference between visibility and invisibility. First,
therefore, some remarks from the devil's (or rather sceptic's)
advocate.
Even alignments to cases like 5, 9, 35, 39, 20, and 24, while
neither major standstills nor full Moons, might have been
recorded. There are many causes of uncertainty in the smaller
details of interpretation of lunar alignments. To take two of a
dozen potentially problematic instances: even after an azimuth
has been converted to a declination, only a combination of an
obliquity and a lunar inclination has effectively been found.
Unless the obliquity is known independently (say from the year)
no conclusion can be drawn about the inclination, and thus none
about its difference from the mean. Secondly, the same alignment
might be ambiguous, for instance, as between the direction of
(1) an actual extreme of type 7, and (2) the only visible Moon
in the neighbourhood of an extreme of type 15 (assuming that the
weather interfered with other observations).
It seems reasonable to suppose that observations were made over
periods of time long enough to stake out correctly alignments to
significant standstills. As for major standstills at the winter
solstice full Moon, they could have been observed wherever an
artificial horizon was created high enough to ensure that the
Sun had well and truly set by the time the Moon rose. It might
have been twilight still, but the Moon would have been visible,
given the right atmospheric conditions.
Which types of lunar alignment are then most likely to have
been favoured? For reasons that have now been explained, the
following three bullets seem most probable:
- Northern lunar setting at first quarter, being more or
less the ideal major standstill. Occurring near spring equinox
(see case 15). Inclination (i) is increased over its mean
value by 8.7' (...). In this context it is intriguing
to recall Pliny's reference to the culling of mistletoe by the
druids on the sixth day of the Moon.
- Southern lunar rising at third quarter, being true major
standstill. Two weeks later than the above, near the spring
equinox (see case 16). Inclination as above, but declination
now negative (south of equator).
- Southern lunar rising or setting at summer full Moon. The
inclination at this type of major standstill is then a minimum
(10.0' below the mean, ...), but the assumption is
that the brightness and general character of full Moon makes
it an attractive proposition.
- The example of Stonehenge, however, recommends a fourth bullet:
Northern lunar rising or setting at winter full Moon. The
inclination is that under bullet 3. Given a regular
horizon such will occur with the Sun above the horizon, but
sunset may be guaranteed either by an artificial horizon or an
unusually high lunar horizon.
These suggestions do not preclude alternatives (such as phases
near full Moon, or cases where the best that can be found over a
short period is for a nondescript phase), but the bullets
listed here do seem inherently more probable than the rest.
There remains the problem of how the perturbation affects minor
standstills. From similar arguments to those given already,
first-quarter spring settings and third-quarter autumn risings
seem intrinsically likely to have attracted attention (as being
near the absolute limit), as do summer full Moons (on account of
their appearance and brightness). Adjustments to the inclination
are exactly as in the corresponding bullets cases for
major standstills, and the corrections in azimuth are of the same
order of magnitude.
Ponting
A point about observing quarter-ish Moons in Ponting ([1981], page70-71): At these phases
the Moon has no illuminated upper limb (or lower limb). A little bit
lower (at least within 0.125 degrees altitude) the Moon is of course
illuminated. Ponting says that this will not be a valid Moon phase
to observe! I think Ponting assumes that the neolithic people knew
the Moon was round and because the upper limb existed but invisible,
they dismissed that shape. I think that neolithic people perhaps did
not (yet) know that the Moon was round, but perhaps they thought it
to be a shape that rotated in the sky (I think one could design such
a shape quiet easily that looks like the Moon when using naked-eye
observations, by rendering an 3D
object).
So I would say that with a quarter-ish Moon, the upper part of the
illuminated Moon shape can be used for observations, see below.
Curtis
Curtis has publish a document on the Calanais I major standstill
limit event [Curtis [2003]). Two things are very interesting
in this document:
- it gives a graph of the apparent altitude for each limit
event, so including a day before and after it. This helps you
plan a trip to Calanais I!
- It gives a nice overview of which lunar phase happens during
the limit events over the seasons. This has great regularity!
Thom
Thom did observations at monuments and documented the declinations
found (necessary when comparing multiple locations). See below
picture from Thom ([1973], page 77):
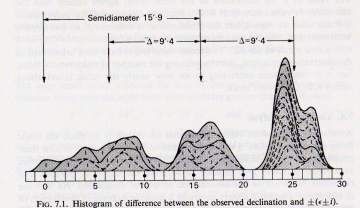 Thom does not talk about different lunar shapes; he even only uses
full Moon shapes in all his figures! So looking at the graph it
seems he is working from the idea that full Moons are observed (semi
diameter is always 15'.9). But the strange things is that
these full Moons are not at the major
declination ±(e±i+D), only quarter Moons are!
Thom does not talk about different lunar shapes; he even only uses
full Moon shapes in all his figures! So looking at the graph it
seems he is working from the idea that full Moons are observed (semi
diameter is always 15'.9). But the strange things is that
these full Moons are not at the major
declination ±(e±i+D), only quarter Moons are!
So it needs more study why Thom did not mention this, as it is
certainly not obvious from his Fig. 2.3 ([1973],
page
20), where full Moons are not near the limits.
It is also clear from Thom ([1973],
page 26, 106 and 110) that he was interested in the maximum of the
perturbation (the perturbation
cycle is 173.31 Days), because that specific moment is a
danger zone for full/new Moons to
become eclipsed, as the Sun is in line with the lunar nodes.
The maximum of the perturbation was only measurable at standstill
limit event due to the methodology proposed by Thom (the
interpolation device; Thom [1973], page
83), although this maximum can be experienced of course at all local
maximum lunar declination events.
Another issue with perception of the max. perturbation moment is of
course the very undetermined behaviour of refraction when apparent
altitude is below 1deg, which can be in the order or larger then the total
perturbation.
It has to be noted that Ruggles ([1999],
page
59) was not able to reproduce the above picture (Fig 7.1) after independent
assessment of horizon notches.
An evaluation
Literature on visibility
According to North, Ponting,
Curtis and some other people, it is in
principle possible to see the set or (and) rise of a Moon's shape
from say 25% illumination at low apparent horizon altitudes (thought
not during day time).
It is planned to change the visibility
program (based on Schaefer [2000])
in such a way that it can also predict the visibility
of the Moon in the sky (and not only in an enclosure).
The below table of lunar phases which happen in general at
(near) major standstill events has been compiled using the
information from Ponting ([1981],
page70-71), North, others and myself. It also
provides ideas about the visibility of the set and rise events
(background color).
|
Major standstill (a)
|
Perturbation (b)
|
Near solar event
|
Rising Moon
|
Setting Moon
|
|
Southern (-e-i)
|
Max. (-D)
|
spring equinox
|

|

|
|
Southern (-e-i)
|
Min. (+D)
|
summer solstice
|

|

|
|
Southern (-e-i)
|
Max. (-D)
|
fall equinox
|

|

|
|
Southern (-e-i)
|
Min. (+D)
|
winter solstice
|

|

|
|
Northern (e+i)
|
Max. (+D)
|
spring equinox
|

|

|
|
Northern (e+i)
|
Min. (-D)
|
summer solstice
|

|

|
|
Northern (e+i)
|
Max. (+D)
|
fall equinox
|

|

|
|
Northern (e+i)
|
Min. (-D)
|
winter solstice
|

|

|
With d=a+b
Red cells are most
probable moments favoured by North
Why are blue cells
not ranked by North? I would rank them also.
Green cells are
less likely, but still possible, I think.
Partly lit Moon
If looking at the effect of the different shapes of the Moon (using
SkyMap to determine the orientation of
the shape) and the experienced maximum azimuth (disregarding
refraction):
- set or rise moments with upper part of illumination
watched:
- With full-ish Moon set and rise, the upper limb is at 0.25°
above the centre of the Moon.
- For third/rising (first/setting) quarter-ish Moon (25-75%),
the upper part of illumination watched could be minimally
0.125° above the centre of the Moon. So the rising (setting)
azimuth could be max. 0.5° more (less) at Calanais I.
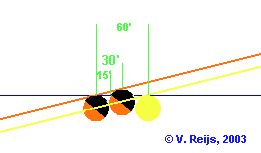
Rise paths of third-quarter and full Moon
each at their min. major azimuth standstill
values
In this case an alignment would differ if one is looking at
first illumination seen or the invisible upper limb of
the Moon at quarter-ish Moons. This changes the distribution of phases and azimuths.
- set or rise moments with bottom part of illumination watched:
- With full-ish Moon set and rise, the lower limb is at 0.25°
below the centre of the Moon.
- For third/rising (first/setting) quarter-ish Moon (25-75%),
the bottom part of illumination watched is 0.25° below the
centre of the Moon. So not different from full-ish Moons.
- meridian transit moments:
For all shapes (25-100%) the upper (or bottom) limb are at 0.25°
above (or below) the centre of the Moon
- reappearing through valley/hole/etc.:
Any part of the Moon could be reappearing, so there is no real
difference looking at any shape of the Moon here.
Theoretical visibility calculations
A graph has been made of the Moon
phase visibility using formula's from Schaefer [2000]:
using formula (12), (10), (9) and (11) to determine just the
Moon illuminance (BMoon) seen on earth. Done for
apparent altitude of 1°, 0.75° and 0.5°.
using formula (35) (with Bsource=B+BMoon)
and (36b) or (36c) (with z=0.2°)
to determine (by iteration) which B just reveals the setting or
rising Moon.
using the table in Schlyter,
horizon brightness at different twilight conditions is
determined.
The below graph is the result (with the following important
parameters; visibility range 20 km, location Ireland, height 60m,
around May, 23 year observer):
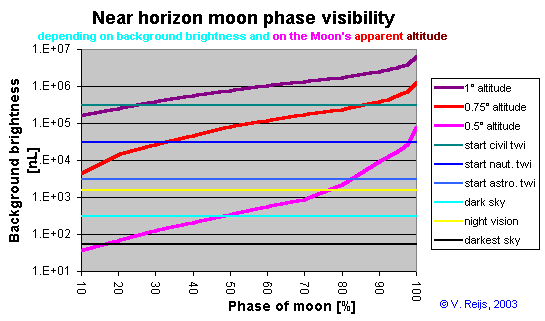
Rule of thumb
Although the variability of the atmosphere makes it hard to predict
what will be visible, one could imagine good days hopefully were
more plentiful in former times;-). At this moment I don't have yet a
final rule of thumb, but based on
some 40 observation to hazy horizons near sea-side here in
Ireland and with apparent altitudes around 0.75°:
- new-ish Moon (say 5-25%) are visible at rise and set when it
is darker than nautical twilight.
An 1.7% Moon was visible at 0.8° apparent altitude at nautical
twilight.
- quarter-ish Moon (25-75%) can be seen rising and setting when
it is darker than cival twilight
- full-ish Moons (75-100%) can be seen setting and rising when
before civil twilight.
This rule of thumb will be updated when more information is gained.
This rule of thumb is mapping the theoretical
model.
Summary on historical/ethnographic
evidence for standstill limit alignments
An overview of an evaluation on historical/ethnographic evidence
made on the HASTO-L list is interesting to read (Bradley
Schaefer [1998]). The conclusion is that there is no evidence of any
historical/ethnographic references on this. Bradley's conclusion on
lunar alignments is:
"This conclusion places a heavy
burden on anyone who claims that a lunar orientation is actually
an alignment, as they must provide evidence of intention when all
evidence shows that no one has any interest at all."
A good list of criteria is given by Schaefer [2004]
concerning alignments (as I call: intentional directions).
The author of
this web page proposes a somewhat changed sequence of criteria
(changes with regard to Schaefer are in purple). Intentional can be by design or
by usage of the monument. The below criteria can also be used by any other discipline
(like archaeoacoustics):
- the astronomical case for
the claimed alignments, or more general; is the case properly evaluated by
the discipline studied.
Schaefer had this criteria as the last criteria in the list,
but criteria A is essential to fulfil, without this no
reason to continue with the following criteria.
- statistical significance over the null hypothesis, where a
multi-site analysis is almost essential (a single site will
never be able to reach a pure statistical significance).
Schaefer [2004]
assumes that minimally a 3 or 4-sigma threshold is needed.
Some null hypothesis are:
- random direction between 0° and 360° (so real null
hypothesis)
- random direction between 0° and 180° or 180° and 360°
- azimuth of random Sun rise and/or set
- azimuth of random Moon rise and/or set
- archaeological information
- historical documents or ethnographic information on the
culture in question or more weakly, ethnographic analogy with
other cultures.
For an analogies, the argument might go something like "Almost
all societies recognize the solstices while many have alignments
to them, so it is plausible to think that a solstitial
orientation observed for a prehistoric monument like Stonehenge
is actually an alignment."
Remember that historical documents can also be a whole new
discipline (like myths or Linear A), and it might be that for
these texts one needs to start again with criteria A in an
iterative way.
An example: We can even transpose Linear A to (for us) normal
text symbols, but we still are not able to interper the
meaning...
- The above criteria B,
C or D might not be the only way, in the humble opinion of the
web master, to proof beyond reasonable doubt that intend is in
place. It is important to be aware that art, positioning in
the sky/sound/landscape, the monuments themselves, etc. all
express intend by people, otherwise why do it!
Such expression are part of this criteria E (which is
comparable with criteria D, but criteria D is restricted to modern type of printed
text). The interpretation might be lacking, but we have the
same problems as in criteria D (compare it with the
interpretation problems about Linear A).
To solve criteria
E, we need to
start for that the particular discipline again with criteria A, in an iterative way (but
not circular way!). The social concept of triangulation
is thus well use-able in this environment [Blesser, 2011,
slide 23].
Further ideas are
welcome.
A paradox
There is a paradox with the above criteria and the actual
classification of some recognized astronomical sites, IMHO.
If there is no possible positive evaluation for criteria D and E
(say for Neolithic, prehistoric monuments), than only criteria B or
C could be used to see if there is astronomical intend. In case
there is no archaeological proof and if the building is unique in
its construction, no progress can be made with the above criteria on
an astronomical alignment:-( Or should we just use analogy under criteria D?
One could say: "It is unique,
and thus the chances are very very
small it is constructed by chance." but that is in most cases
not a valid deduction.
IMHO there is a paradox between these five criteria and looking at
what people recognize as astronomically aligned monuments. A lot of
pre-historic unique buildings (like Newgrange, Stonehenge, etc.) are
recognized as being built by intend with astronomical guidelines. I
don't think this is due to criteria B, C, D or E... So why are these
buildings still recognized as being astronomically aligned by
intend?
To be honest, I think that it should be possible to see a unique
construction (and lacking B, C, D and E criteria) as astronomically
important. A present day example: a cathedral is unique, and it
stands for something that is made by intend.
So I am in principle using the analogy part of criteria D, which is
very dangerous, I know.
Putting my paradox in another way:
- some people (Schaefer, but also myself sometimes; that is why
it is a paradox of mine) want to see proof by using statistics
(if no other criteria applies); if many buildings have a
possible celestial direction it might be an alignment by intend.
- A lot of recognized
alignments are though very unique (like Newgrange, Stonehenge,
Hopi, etc.), so statistics are not applicable. But these
buildings seem to be recognized
by the establishment to have accepted alignments. So by what
methodology are they defined as an alignment by intend?
For me both principles are valid. So there is a gap in the above
criteria.
Why and when to witness celestial (lunar)
events.
Several reasons can be heard for why and when to witness a celestial
(lunar) event:
- when real full Moon
- when full-ish Moon
- when quarter-ish Moon
- when maximum (geocentric) declination
- when azimuth or altitude are maximum or minimum
- at set, rise and/or transit times
- at northern and/or southern standstill events
- when greatest possibility of good weather
- at a certain location and horizon profile
- when in (holiday) break
- when a trip is organized
- for scientific of ceremonial use
- due to a certain ideology/religion/etc.
- it is mystical/logical that neolithic might be interested in
such events
- fits into the frame of mind of a person<>
- If people have additional reasons to celebrate an lunar/solar
event, let me know.
The above reasons are all valid. The above reasons are used at
present, so I am sure that all these reasons (and more) were also
used in pre-historic times (and thus perhaps fixed in a neolithic
monument).
Any reason is a valid intend/experience, because the reason can be
the driver for human action (even if it is scientifically not
correct).
Azimuth value of major azimuth
standstill events in ~3000 BCE
The azimuths values of major azimuth standstill events in
~3000 BCE have different value than at
present (~2000 CE) dates due to change in obliquity. For the Calanais
I location this has an 2.4° influence on the azimuth, which has an
influence of some 0.6° on the apparent altitude.
Major azimuth standstill dates until
2100
The following apparent major azimuth standstill
events are calculated for dates around the major standstill limit
and for the location of Calanais I (the shape of the Moon
has not been evaluated in this appendix). Also an evaluation of
the top10 major standstill events is given:
Different latitude and/or longitude provide different sequence of
dates. See a web-page show how to get the
JPL data.
Help for determining the apparent
standstill limit events
One can make one's own overview of set/rise dates of the Moon near
their major/minor standstill limit. A web-page show how to get the JPL data. Alternative software to do
these evaluations is based on ARCHAECOSMO and swephR.
If one follows the above given method (don't forget to fill in the
longitude, latitude and height of the location you want to see), one
gets an e-mail back from JPL with all the set and rise times.
Save and rename the e-mail content to a file with extension .csv.
Start you spreadsheet program (like Excel) and get the text file in
it using File -> Open... with File of type: Text files *.txt
and use Delimited option
with Comma delimiters and
Finish for opening the
file. When the file is in the spreadsheet, select the whole
worksheet and then Data
-> Sort... on the Column D (Azi_ column).
This results in an ordered file, where one can see which dates are
the limit dates.
Acknowledgments
I would like to thank the following people for their help and
constructive feedback: and all other unmentioned people. Any
remaining errors in methodology or results are my responsibility
of course!!! If you want to provide constructive feedback, let me know.
Disclaimer and Copyright
 Home
Home Up
Up Search
Search Mail
Mail
Major content related changes: January 2, 2023




 or
or 
 or
or